量子ゲート制御 | 曽我部研究室 SogabeLab 国立大学法人電気通信大学│AI 人工知能 量子
RESEARCH
研究内容
量子ゲート制御
量子の不確実性と、人工知能の異次元の融合
~量子回路設計の新たなプロジェクト始動~
◆量子部分観測マルコフ決定過程を実機量子コンピュータで実装と検証
◆量子分野とAI分野を融合し、量子回路(※1)設計に新たな展開
電気通信大学の曽我部研究室(基盤理工学専攻)は強化学習(※2)、量子アルゴリズム(※3)、量子強化学習(※4)を基幹テーマとして研究を行っています。量子の不確実性(※5)と人工知能の技術を融合した「量子部分観測マルコフ決定過程(※6)による量子回路設計」に関する研究が独立行政法人情報処理推進機構2021年度未踏ターゲット事業の一環として新たな展開に向かっています。
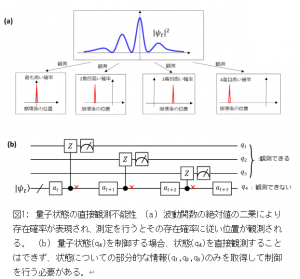
量子コンピュータは「ゲート方式」と「アニーリング(※7)方式」の二つの方式があります。「ゲート方式」は汎用型の量子コンピュータであり、基本的な量子ゲートを組み合わせた量子回路を構築し計算を行います。量子ゲート回路の設計は、これまで古典コンピュータシミュレーションにより最適化を行ってきましたが、量子ビットの数が多くなると計算量が指数的に増えてしまうという問題がありました。より多くの量子ビットに対して回路設計を考えるには実機の量子コンピュータを使う必要があります。しかし、実機の量子コンピュータを使って制御と最適化を行うには、「波動関数の崩壊(※8)により量子状態を直接観測・制御することはできない」という量子力学の壁を克服しないと実現できません(図1)。
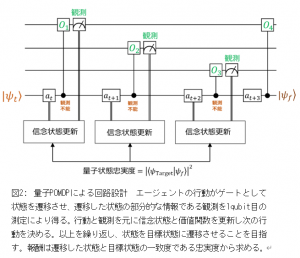
今回のプロジェクトでは、本研究室が得意とする強化学習の手法を活かし、「量子状態の直接観測不能」という問題を部分観測マルコフ決定過程(POMDP)問題に変換した、量子部分観測マルコフ決定過程(量子POMDP)手法の開発に取り組みます*1。量子POMDP理論の枠組みの一つは、2014年にMITのAaronson教授により密度行列(※9)を用いて提唱されていますが、未だ理論的な研究段階にとどまり、実用的なアルゴリズムはまだ確立されていません。我々は世界で初めて量子MDP理論を実機で演算できる量子回路モデルの開発に成功しており、本プロジェクトでは量子MDP回路モデルをさらに拡張した量子POMDP理論モデルを実装し、シミュレータと実機を活用して量子回路設計を行い、開発手法の性能を評価します (図2)。これにより現在の最速の古典スーパーコンピュータの1億倍もの処理能力を誇るとされる量子コンピュータ開発の最大の難所といわれる量子回路の設計において大きく貢献することが期待されます。
本プロジェクトは、曽我部研究室の部分観測強化学習に精通する木村友彰(基盤理工学専攻博士前期2年)が、上記の内容に基づき独立行政法人情報処理推進機構(IPA)2021年度未踏ターゲット事業の「量子コンピューティング技術を活用したソフトウェア開発分野」に応募し採択たものです。
用語説明
- 量子回路: 基本的な量子ゲートの組み合わせにより量子アルゴリズムを記述するもの。
- 強化学習: 動的に変化する環境で最適な意思決定を学習する機械学習手法。
- 量子アルゴリズム: 量子コンピュータで実行されるアルゴリズム。広い意味では量子と古典を組み合わせたハイブリッドアルゴリズムも含む。
- 量子強化学習: 強化学習に量子コンピュータの技術を取り入れ、古典コンピュータを用いた強化学習を超える高性能化を目指した学習手法。
- 量子の不確実性: 量子力学では原子は波と粒子の性質を併せ持つ。測定するまでは位置が確率的に決まる波の性質をもち、粒子の位置を確定することはできない。
- 部分観測マルコフ決定過程: マルコフ決定過程でエージェントが受け取っていた状態が完全に取得できず、エージェントが受け取る情報がマルコフ性を満たすとは限らない確率過程。
- アニーリング: 高温にした金属をゆっくり冷やすと最小エネルギー状態を保持した安定構造となる現象。この現象を模して、ゆっくり冷やす代わりに量子ビットにかける横磁場の強さをゆっくり下げて計算するのがアニーリング方式の量子コンピュータである。
- 波動関数の崩壊: 波動関数の絶対値の二乗によって確率的に表現されていた原子の位置が測定により確定する。
- 密度行列: 量子力学において、混合状態を表すために用いる行列。
