August 2022 | 曽我部研究室 SogabeLab 国立大学法人電気通信大学│AI 人工知能 量子

Title

Energetics at the Surface of Photoelectrodes and Its Influence on the Photoelectrochemical Properties

📄Resource　

https://pubmed.ncbi.nlm.nih.gov/26722780/

J. Phys. Chem. Lett. 2015, 6, 4083−4088

🔎Points

論文を選択した理由(目的)
1)電解液と光電極の界面の理解することが重要
光起電力と関係のバンド図を用いた説明がある。
2)Hematite(α-Fe2O3)のバンド図と光起電力の関係
さらに、実験結果がある。
掲載された図について、説明する。
Fig.1　光水分解の概要
a)陽極での光吸収とキャリア分離のバンド様子
b)電気分解槽と電極の配置の様子
陽極で酸素
陰極で水素
c)表面にhematiteがある or、なしのバンド図
=>広がった表面準位が存在する様子
d)Bare-hematiteに対して、触媒がある場合のJ-Vグラフ
Fig.2 表面でのバンド図
a)Fermi-level pinning なし
b)Fermi-level pinning あり
Fig.3 光有と光無での電流密度―電圧特性
=>Bare-hematiteより早く電流が流れます。
=>O2/H2Oレベルが近いことを示す。Fig.4 開放状態での電圧測定により得られるバンド図
a)理想条件において、開放回路での暗状態と明状態でのバンド図の違い
b)非線形要因などにより光電圧が減少
ヘルムホルツ電気二重層内に期待しない電圧降下が発生する。
この電気二重層により電解液に過電圧となる電圧降下が発生する。
c) 開放回路における光ありと光なしの測定結果
フェルミ準位ピンイングがないとき、案状態で1.23V(RHE)になる。
サンプル
3:ALD hematite with NiFeOx
5:Regraoeth hematite nanorod with NiFeOx
1:ALD hematite
[[まとめ]]
Hematieの研究結果でのヘルムホルツ層での電圧降下は、TiO2でも再現される。
光電極における触媒の集積化は、重要な対策として再認識される。
しかし、界面での性質は、詳細に研究されていない。
界面でのエネルギーと反応がどの様に変化するかは、研究対象とし価値がある。

💬Questions or comments

以下の我々の実験環境における違いは？
1)光源がハロゲンの場合は？
=>短波がない場合　=> 電流密度が下がるだけの同じ結果になる？
2)電解液のpHの影響は？
=>pH=7の場合 => V(RHV)のシフトのみか？

---

Title

Enabling unassisted solar water splitting by iron oxide and silicon

📄Resource https://www.nature.com/articles/ncomms8447/

Nat.Commun. 2015, 6, 7447
DOI: 10.1038/ncomms8447

🔎Points

論文を選択した理由(目的)
上記で紹介した実験報告(Fig.3, Fig4.c)であり詳細な説明がある。
Hematiteを使用した自己バイアスでの光電気分解の実験結果がある。
*試料について
FTO上にFeOOHを成長後、800℃で1h加熱
掲載された図について、説明する。
Fig.1<<===我々の実験に関連する興味ある実験結果
改善したターンオン特性でのHematite
a)
光有と無での電流密度-電圧特性
Bare hematiteに対して
=>表面修飾したhematiteは、
ON電圧が減少している
b)バンド図の変化の様子
hematiteと再成長の違い
c)光無と光有での開放電圧
Fig.2 実験結果の図
a)結晶性は、XRDで調査
b)Ramanから表面での結合状態を調査
c)X-ray absorption spectra(XAS)で酸素の結合状態を調査
Fig.3　Morphology変化
SEM像=>表面構造
a),b),c),d)
透過電子像
e),f),g),h)
=>断面像, Rod状である。
Fig.4 アシストなし水分解
a)電極の様子
短波をFe2O3で吸収して、
透過した光を陰極のTiO2/Pt付きa-Siで吸収
AM1.5 ONE-SUN照射
b)時間と電流の関係
Phosphte solution(pH=11.8)
リン酸塩緩衝液
10時間でも一定電流を示した。
[[まとめ]]
自己バイアス型光電気分解において
変換効率0.91%を得た。
さらに、
大きな光電流を得た。
J=4.32mAcm-2 at 1.23V(RHE)
簡単な再成長方法が有効である可能性を示した。

💬Questions or comments

1)実際のサイズは？
小さいサンプルでは、電流密度が大きくできる可能性あり。

2)オーミック電極の作製方法は？
複雑な工程を含む難しい加工が必要な場合がある。

---

Title

Warmstarting column generation for unit commitment
Nagisa Sugishita, Andreas Grothey, Ken McKinnon

📄Resource  https://arxiv.org/abs/2110.06872

🔎Points

• 大規模な最適化問題を高速で求解するため、Dantzig-Wolfe分解を用いて変形した最適化問題に対して最初から最適解に近い暫定解を与える手法（warm start）が紹介されている
• 発電機起動停止問題（UCP）では、実用的には発電機性能を示す定数は使い回し需要等一部の想定のみが変わった問題を繰り返し解く。そのため発電機のセットに対して暫定解のパラメータの組を学習・推定できるとしている
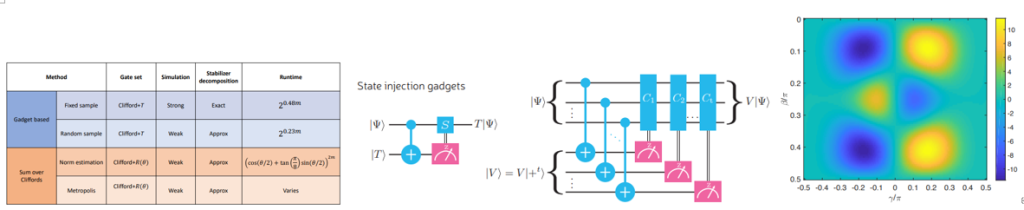
• 発電機を200/600/1000台並列で動かす大規模なUCPに対して暫定解を推定する手法として深層学習、ランダムフォレスト、最近傍探索、LPR（Dantzig-Wolfe分解と結びついた推定手法）で比較している。添付図では、各手法の中でも特に深層学習はいずれの場合に対しても短い時間で解決することができることを示している

💬Questions or comments

---

Title

Enhancing photoelectrochemical water splitting by combining and heterojunction engineering
NATURE COMMUNICATIONS, (2019)

Kai-Hang Ye, Haibo Li, Duan Huang, Shuang Xiao, Weitao Qio, Mingyang Li, Yuwen Hu, Wenjie Mai, Hongbing Ji & Shihe Yang

📄Resource  https://doi.org/10.1038/s41467-019-11586-y

🔎Points

1.   この論文では半導体電極を用いた水の光分解の効率向上のための2つのユニークな戦略が紹介されている。
2.   第一は、電極(BiVO4)にMoをドープすることで仕事関数を変化させ、界面のエネルギー損失を減少させ、開放起電力を増加出来ること。ここではMoのドープ量を1%以下で変化させることで立ち上がり電位を最小化した。また0.1%Mo- BiVO4電極でMoをドープしていない電極よりも8％程、光電流値が増加した。ここで用いられている電極(BiVO4)は化学的手法で作製されている。
3.   第二にBドープC3N4とMoドープBiVO4のヘテロ接合創製と最適化がC3N4にBドープすることで仕事関数を調整し実行され、B- C3N4とMo-BiVO4界面での光生成された電子-正孔対の分離を大幅に促進することに成功した。0.05％、0.1％0Moドープした電極において立ち上がり電位がおよそ0.1V負にシフトした。
4.   これらを実施したことで電極の立ち上がり電位を減少させ、BiVO4ベース光アノードでの電荷分離や光学特性を改善し、RHEに対して0.54Vで2.67%の量子効率を得た。これらの研究結果は次世代の光電極作製への大きな指針になりうる。

💬Questions or comments

1.   ヘテロ接合型電極においてそれぞれの層にドーピングをすることで界面に生じる障壁の高さを変化させ光生成キャリアの移送速度を改善し、仕事関数を調整することでそれぞれのバンド端位置を変化させる手法に魅力を感じた。
2.   ドーピングすることにより光電流密度の増加はある程度実現したが電極の寿命の改善など、実用化までまだまだ改善すべき点は多い。

---

Title

Simulation of quantum circuits by low-rank stabilizer decompositions
Sergey Bravyi, Dan Browne, Padraic Calpin, Earl Campbell, David Gosset, and Mark Howard

📄Resource　https://quantum-journal.org/papers/q-2019-09-02-181/

🔎Points

1. State-of-the-art stabilizer simulator for quantum circuits.

💬Questions or comments

1. This is about simulation of quantum circuits using classical computers. If a quantum circuit can be efficiently simulated by some classical algorithm, then people may consider there is no quantum advantage for that quantum circuit.
2. Gottesman-Knill theorem (arXiv.quant-ph/9807006) proves that stabilizer circuits can be efficiently simulated by a classical method. Based on this idea, Aaronson and Gottesman (Phys. Rev. A 70, 052328 (2004)) developed a stabilizer simulator algorithm. This new paper by Bravyi et al. is a further development and summary.

---

Title

Stanko, Silvestr, and Karel Macek. “Risk-averse Distributional Reinforcement Learning: A CVaR Optimization Approach.” IJCCI. 2019.

📄Resource　https://pdfs.semanticscholar.org/6fb3/2ea018eff2d394461b4d4f22db855933f984.pdf

🔎Points

• 強化学習の学習ステップにおいてQ値ではなくCVaRを用いた最適化について、Value Iteration, Q-Learning, DQNでの学習法を提案している。
• 従来のCVaRを用いたValue Iterationに比べ, 計算時間を改善している。(多項式時間から線形時間へ)

💬Questions or comments

• 学習後報酬分布のα分位点におけるCVaRの値を元にしたPolicyを使うことができ、様々な分位点での状態価値や状態行動価値を比較することができる。
• どの分位点におけるCVaRを用いたPolicyが最適なのかをどのように判断するか。
• 離散アクションのアルゴリズムに組み込むことができたが、DDPGなどの連続アクションを取れるRLアルゴリズムに拡張することはできるのか。

---

Title

Efficient inorganic solid solar cell composed of perovskite and PbS quantum dots

📄Resource　https://pubs.rsc.org/en/content/articlelanding/2015/nr/c5nr00420a/unauth

🔎Points

・Perovskiteをtwo-step法で作成し、ホール輸送層にPbS量子ドットを加えた場合に電力変換効率が7.88%を達成した。
・作成した太陽電池の電力変換効率は2日目以降も作成直後の8%程度の減衰で性能が維持されていることから、比較的安定性が高いことを示した。

💬Questions or comments

・PbS量子ドットの粒径が違うものを使用した場合にはどのように電力変換効変化するのか気になった。
・PbS量子ドットを入れた場合に吸光度が少し増加していたので、電力変換効率の増加に寄与しているのではないかと感じた。

---

Title

Inverse Temperature Dependence of Charge Carrier Hopping in Quantum Dot Solids

Rachel H.Gilmore.et.al,ACS Nano 2018, 12, 8, 7741–7749

📄Resource　https://doi.org/10.1021/acsnano.8b01643

🔎Points

・単分散QD固体における局在状態のホッピング輸送が温度の低下とともに移動度が高くなることを過渡吸収分光法、微小角入射X線散乱法（GISAXS）、および数値モデリングを用いて示した
・量子ドットの移動度が温度が上がることによって下がるのは、温度が上がることによる量子ドット間の距離が離れる影響であることを突き止めた
・量子ドットのホッピング現象の数値モデルを作成し、パラメーターを実験結果から求めることで電荷キャリアのダイナミクスのモデルを作り出した
・KMCシュミレーションを用いて、移動度の算出が行われており、実験と同様の傾向を示されている

💬Questions or comments

・KMCシュミレーションで移動度を求めていたが、その部分の詳細な説明がなかったため、その部分の説明もしてほしかった
・実験結果を用いて、数値モデルのパラメーターのフィッティングを行っていたが、自分で仮にモデルを作成する場合、その部分はDFTの計算結果を用いて行うのか
・温度によって、量子ドットの輸送の仕方がホッピングかバンドと変わると書いてあるが、電子輸送のキャリアダイナミックスをホッピングモデルのみで示しているのが疑問に思った

---

Title

“Quantum reinforcement learning : the maze problem”
Nicola Dalla Pozza, Lorenzo Buffoni, Stefano Martina, Filippo Caruso
Quantum Machine Intelligence 4, Article number: 11 (2022)

📄Resource　https://doi.org/10.1007/s42484-022-00068-y

🔎Points

1. 量子機械学習は量子情報と機械学習が融合した若い分野であるが、現在急速に発展している。その中でも本論文では強化学習の考えをもとに、これを量子領域に応用する量子強化学習（QRL）の考え方を示した。
2. QRLと古典的なディープニューラルネットワークを組み合わせることで、エージェントが古典的な領域と量子的な領域の両方で最適な戦略を学習することを見出し、またノイズの多い環境では量子的な高速化からエージェントが非常に短い時間スケールでも有用な行動を行なった。

💬Questions or comments

1. 新時代の量子情報処理技術において高い伝送速度と量子エラー訂正などの異なるタスクを実行するために応用できる可能性があると感じました。
2. 現在のNISQ時代における強化学習の量子領域への応用として面白い研究だと思いました。

---

Title

📄Resource　　

🔎Points

💬Questions or comments

---

Title

📄Resource　　

🔎Points

💬Questions or comments

---

Title

📄Resource　　

🔎Points

💬Questions or comments